|
Degrees of Freedom
Author(s)
David M. Lane
Prerequisites
Measures
of Variability, Introduction to Estimation
Learning Objectives
- Define degrees of freedom
- Estimate the variance from a sample of 1 if the population mean is
known
- State why deviations from the sample mean are not independent
- State the general formula for degrees of freedom in terms of the number
of values and the number of estimated parameters
- Calculate s2
Some estimates are based on more information than
others. For example, an estimate of the variance based on a sample
size of 100 is based on more information than an estimate of the
variance based on a sample size of 5. The degrees of freedom (df)
of an estimate is the number of independent pieces of information
on which the estimate is based.
As an example, let's say that we know that the
mean height of Martians is 6 and wish to estimate the variance
of their heights. We randomly sample one Martian and find that
its height is 8. Recall that the variance is defined as the
mean squared deviation of the values from their population mean.
We can compute the squared deviation of our value of 8 from
the population mean of 6 to find a single squared deviation
from the mean. This single squared deviation from the mean, (8-6)2
= 4, is an estimate of the mean squared deviation for all Martians.
Therefore, based on this sample of one, we would estimate that
the population variance is 4. This estimate is based on a single
piece of information and therefore has 1 df. If we sampled another
Martian and obtained a height of 5, then we could compute a
second estimate of the variance, (5-6)2 =
1. We could then average our two estimates (4 and 1) to obtain
an estimate of 2.5. Since this estimate is based on two independent
pieces of information, it has two degrees of freedom. The two
estimates are independent because they are based on two independently
and randomly selected Martians. The estimates would not be independent
if after sampling one Martian, we decided to choose its brother
as our second Martian.
As you are probably thinking, it is pretty rare
that we know the population mean when we are estimating the variance.
Instead, we have to first estimate the population mean (μ)
with the sample mean (M). The process of estimating the mean affects
our degrees of freedom as shown below.
Returning to our problem of estimating the variance
in Martian heights, let's assume we do not know the population
mean and therefore we have to estimate it from the sample. We
have sampled two Martians and found that their heights are 8
and 5. Therefore M, our estimate of the population mean, is
M = (8+5)/2 = 6.5.
We can now compute two estimates of variance:
Estimate 1 = (8-6.5)2
= 2.25
Estimate 2 = (5-6.5)2 = 2.25
Now for the key question: Are these two estimates
independent? The answer is no because each height contributed
to the calculation of M. Since the first Martian's height of 8 influenced
M, it also influenced Estimate 2. If the first height had been,
for example, 10, then M would have been 7.5 and Estimate 2
would have been (5-7.5)2 = 6.25 instead
of 2.25. The important point is that the two estimates are not
independent and therefore we do not have two degrees of freedom.
Another way to think about the non-independence is to consider
that if you knew the mean and one of the scores, you would know
the other score. For example, if one score is 5 and the mean is
6.5, you can compute that the total of the two scores is 13 and
therefore that the other score must be 13-5 = 8.
In general, the degrees of freedom for an estimate
is equal to the number of values minus the number of parameters
estimated en route to the estimate in question. In the Martians
example, there are two values (8 and 5) and we had to estimate
one parameter (μ) on the way to estimating the parameter of
interest (σ2). Therefore, the estimate
of variance has 2 - 1 = 1 degree of freedom. If we had sampled
12 Martians, then our estimate of variance would have had 11 degrees
of freedom. Therefore, the degrees of freedom of an estimate of
variance is equal to N - 1, where N is the number of observations.
Recall from the section on variability
that the formula for estimating the variance in a sample is:
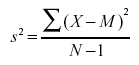
The denominator of this formula is the degrees
of freedom.
Please answer the questions:
|