|
|
Exercises
Author(s)
David M. Lane
Prerequisites
All material presented in the Normal Distributions chapter
Selected answers
You may want to use the "Calculate
Area for a given X" and the "Calculate
X for a given Area" applets for some of these
exercises.
- If scores are normally distributed with a mean of 35 and
a standard deviation of 10, what percent of the scores is:
(a) greater than 34? (b) smaller than 42? (c) between 28 and
34? (relevant section)
- (a) What are the mean and standard deviation of the standard
normal distribution? (b) What would be the mean and standard
deviation of a distribution created by multiplying the standard
normal distribution by 8 and then adding 75? (relevant
section & here)
- The normal distribution is defined by two parameters.
What are they?
(relevant section)
- (a) What proportion of a normal distribution is within
one standard deviation of the mean? (b) What proportion is
more than 2.0 standard deviations from the mean? (c) What proportion
is between 1.25 and 2.1 standard deviations above the mean?
(relevant section)
- A test is normally distributed with a mean of 70 and a
standard deviation of 8. (a) What score would be needed to
be in the 85th percentile? (b) What score would be needed to
be in the 22nd percentile? (relevant
section)
- Assume a normal distribution with a mean of 70 and a standard
deviation of 12. What limits would include the middle 65% of
the cases? (relevant section)
- A normal distribution has a mean of 20 and a standard
deviation of 4. Find the Z scores for the following numbers:
(relevant section) (a)
28 (b) 18 (c) 10 (d)
23
- Assume the speed of vehicles along a stretch of I-10 has
an approximately normal distribution with a mean of 71 mph
and a standard deviation of 8 mph.
- The current speed limit is 65 mph. What is the proportion
of vehicles less than or equal to the speed limit?
- What
proportion of the vehicles would be going less than 50
mph?
- A new speed limit will be initiated such that approximately
10% of vehicles will be over the speed limit. What is
the new speed limit based on this criterion?
- In what way
do you think the actual distribution of speeds differs
from a normal distribution?
(relevant section)
- A variable is normally distributed with a mean of 120
and a standard deviation of 5. One score is randomly sampled.
What is the probability it is above 127? (relevant
section)
- You want to use the normal distribution to approximate
the binomial distribution. Explain what you need to do to find
the probability of obtaining exactly 7 heads out of 12 flips.
(relevant section)
- A group of students at a school takes a history test.
The distribution is normal with a mean of 25, and a standard
deviation of 4. (a) Everyone who scores in the top 30% of the
distribution gets a certificate. What is the lowest score someone
can get and still earn a certificate? (b) The top 5% of the
scores get to compete in a statewide history contest. What
is the lowest score someone can get and still go onto compete
with the rest of the state? (relevant
section)
- Use the normal distribution to approximate the binomial
distribution and find the probability of getting 15 to 18 heads
out of 25 flips. Compare this to what you get when you calculate
the probability using the binomial distribution. Write your
answers out to four decimal places. (relevant
section & relevant
section)
- True/false: For any normal distribution, the mean, median,
and mode will have the same value. (relevant
section)
- True/false: In a normal distribution, 11.5% of scores
are greater than Z = 1.2. (relevant
section)
- True/false: The percentile rank for the mean is 50%
for any normal distribution. (relevant
section)
- True/false: The larger the π, the better the normal
distribution approximates the binomial distribution. (relevant
section & relevant
section)
- True/false: A Z-score represents the number of standard
deviations above or below the mean. (relevant
section)
- True/false: Abraham de Moivre, a consultant
to gamblers, discovered the normal distribution when trying
to approximate the binomial distribution to make his computations
easier. (relevant section)
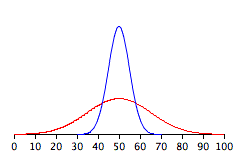
- True/false: The standard deviation of the blue distribution
shown below is about 10. (relevant
section)
- True/false: In the figure below, the red distribution
has a larger standard deviation than the blue distribution.
(relevant section)
- True/false: The red distribution has more area underneath
the curve than the blue distribution does. (relevant
section)
Questions from Case Studies:
The following question uses data from the Angry
Moods (AM)
case study.
- For this problem, use the Anger Expression (AE) scores.
(a) Compute the mean and standard deviation. (b) Then, compute
what the 25th, 50th and 75th percentiles would be if the distribution
were normal. (c) Compare the estimates to the actual 25th,
50th, and 75th percentiles. (relevant
section)
The following question uses data from the Physicians'
Reactions (PR)
case study.
- For this problem, use the time spent with the overweight
patients. (a) Compute the mean and standard deviation of
this distribution. (b) What is the probability that if you
chose an overweight participant at random, the doctor would
have spent 31 minutes or longer with this person? (c) Now assume
this distribution is normal (and has the same mean and standard
deviation). Now what is the probability that if you chose an
overweight participant at random, the doctor would have spent
31 minutes or longer with this person? (relevant
section)
The
following questions are from ARTIST (reproduced with permission)

Visit the site
- A set of test scores are normally distributed. Their mean
is 100 and standard deviation is 20. These scores are converted
to standard normal z scores. What would be the mean and median
of this distribution?
a. 0
b. 1
c. 50
d. 100
- Suppose that weights of bags of potato chips coming from
a factory follow a normal distribution with mean 12.8 ounces
and standard deviation .6 ounces. If the manufacturer wants
to keep the mean at 12.8 ounces but adjust the standard deviation
so that only 1% of the bags weigh less than 12 ounces, how
small does he/she need to make that standard deviation?
- A student received a standardized (z) score on a test that
was -. 57. What does this score tell about how this student
scored in relation to the rest of the class? Sketch a graph
of the normal curve and shade in the appropriate area.
- Suppose you take 50 measurements on the speed of cars on
Interstate 5, and that these measurements follow roughly a
Normal distribution. Do you expect the standard deviation of
these 50 measurements to be about 1 mph, 5 mph, 10 mph, or
20 mph? Explain.
- Suppose that combined verbal and math SAT scores follow
a normal distribution with mean 896 and standard deviation
174. Suppose further that Peter finds out that he scored
in the top 3% of SAT scores. Determine how high Peter's score
must have been.
- Heights of adult women in the United States are normally
distributed with a population mean of μ =
63.5 inches and a population standard deviation of σ =
2.5. A medical researcher is planning to select a large
random sample of adult women to participate in a future study.
What is the standard value, or z-value, for an adult woman
who has a height of 68.5 inches?
- An automobile manufacturer introduces a new model that averages
27 miles per gallon in the city. A person who plans to purchase
one of these new cars wrote the manufacturer for the details
of the tests, and found out that the standard deviation is
3 miles per gallon. Assume that in-city mileage is approximately
normally distributed.
- What is the probability that the person will purchase
a car that averages less than 20 miles per gallon for in-city
driving?
- What is the probability that the person will purchase
a car that averages between 25 and 29 miles per gallon for
in-city driving?
Answers:
1) (b) 75.8%
2) (b) Mean = 75
4) (c) .088
5) (a) 78.3
7) (a) 2.0
8) (a) .227
11) (a) 27.1
12) .2037 (normal approximation)
22) 25th percentile: (b) 28.27 (c) 26.75
23) (b) .053
Please answer the questions:
|
|