|
Sampling Distribution of p
Author(s)
David M. Lane
Prerequisites
Introduction
to Sampling Distributions, Binomial
Distribution, Normal
Approximation to the Binomial
Learning Objectives
- Compute the mean and standard deviation of the sampling distribution
of p
- State the relationship between the sampling distribution of p and the
normal distribution
Assume that in an election race between Candidate
A and Candidate B, 0.60 of the voters prefer Candidate A. If a random
sample of 10 voters were polled, it is unlikely that exactly 60%
of them (6) would prefer Candidate A. By chance the proportion
in the sample preferring Candidate A could easily be a little
lower than 0.60 or a little higher than 0.60. The sampling distribution of p is the distribution that would result
if you repeatedly sampled 10 voters and determined the proportion
(p) that favored Candidate A.
The sampling distribution of p is a special case
of the sampling distribution of the mean. Table 1 shows a hypothetical
random sample of 10 voters. Those who prefer Candidate A are given
scores of 1 and those who prefer Candidate B are given scores of 0.
Note that seven of the voters prefer candidate A so the sample
proportion (p) is
p = 7/10 = 0.70
As you can see, p is the mean of the 10 preference
scores.
Table 1. Sample of voters.
|
Voter
|
Preference
|
|
1
|
1
|
|
2
|
0
|
|
3
|
1
|
|
4
|
1
|
|
5
|
1
|
|
6
|
0
|
|
7
|
1
|
|
8
|
0
|
|
9
|
1
|
|
10
|
1
|
The distribution of p is closely related to the
binomial distribution. The binomial distribution is the distribution
of the total number of successes (favoring Candidate A, for example)
whereas the distribution of p is the distribution of the mean
number of successes. The mean, of course, is the total divided
by the sample size, N. Therefore, the sampling distribution of
p and the binomial distribution differ in that p is the mean of
the scores (0.70) and the binomial distribution is dealing with
the total number of successes (7).
The binomial distribution has a mean of
μ = Nπ
Dividing by N to adjust for the fact that the
sampling distribution of p is dealing with means instead of totals,
we find that the mean of the sampling distribution of p is:
μp = π
The standard deviation of the binomial distribution
is:
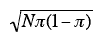
Dividing by N because p is a mean not a total,
we find the standard error of p:
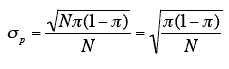
Returning to the voter example, π = 0.60 and N = 10. (Don't
confuse π = 0.60, the population proportion and p = 0.70, the
sample proportion.) Therefore, the mean of the sampling
distribution of p is 0.60. The standard error is

The sampling distribution of p is a discrete rather
than a continuous distribution. For example, with an N of 10,
it is possible to have a p of 0.50 or a p of 0.60 but not a p
of 0.55.
The sampling distribution of p is approximately
normally distributed if N is fairly large and π is not close
to 0 or 1. A rule of thumb is that the approximation is good
if both Nπ and N(1 - π) are greater than 10. The
sampling distribution for the voter example is shown in Figure
1. Note that even though N(1 - π) is only 4, the approximation
is quite good.
Please answer the questions:
|