|
Sampling Distribution of Difference Between
Means
Author(s)
David M. Lane
Prerequisites
Sampling
Distributions, Sampling
Distribution of the Mean, Variance
Sum Law I
Learning Objectives
- State the mean and variance of the sampling distribution of the difference
between means
- Compute the standard error of the difference between means
- Compute the probability of a difference between means being above a
specified value
Statistical analyses are very often concerned
with the difference between means. A typical example is an experiment
designed to compare the mean of a control group with the mean
of an experimental group. Inferential statistics used in the analysis of this type of experiment
depend on the sampling distribution of the difference between
means.
The sampling distribution of the difference between
means can be thought of as the distribution that would result
if we repeated the following three steps over and over again:
(1) sample n1 scores from Population
1 and n2 scores from Population 2, (2)
compute the means of the two samples (M1
and M2), and (3) compute the difference between
means, M1 - M2.
The distribution of the differences between means is the sampling
distribution of the difference between means.
As you might expect, the mean of the sampling distribution
of the difference between means is:

which says that the mean of the distribution
of differences between sample means is equal to the difference
between population means. For example, say that the mean test score
of all 12-year-olds in a population is 34 and the mean of 10-year-olds is 25. If numerous samples were taken from each age group
and the mean difference computed each time, the mean of these
numerous differences between sample means would be 34 - 25 =
9.
From the variance
sum law, we know that:
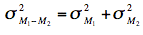
which says that the variance of the sampling
distribution of the difference between means is equal to the
variance of the sampling distribution of the mean for Population
1 plus the variance of the sampling distribution of the mean
for Population 2. Recall the formula for the variance of the
sampling distribution of the mean:

Since we have two populations and two samples sizes,
we need to distinguish between the two variances and sample sizes.
We do this by using the subscripts 1 and 2. Using this convention,
we can write the formula for the variance of the sampling distribution
of the difference between means as:

Since the standard error of a sampling distribution is the standard
deviation of the sampling distribution, the standard error of
the difference between means is:
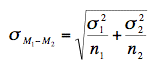
Just to review the notation, the symbol on the
left contains a sigma (σ), which means it is a standard deviation.
The subscripts M1 - M2
indicate that it is the standard deviation of the sampling distribution
of M1 - M2.
Now let's look at an application of this formula.
Assume there are two species of green beings on Mars. The mean
height of Species 1 is 32 while the mean height of Species 2 is
22. The variances of the two species are 60 and 70, respectively
and the heights of both species are normally distributed. You
randomly sample 10 members of Species 1 and 14 members of Species
2. What is the probability that the mean of the 10 members of
Species 1 will exceed the mean of the 14 members of Species 2
by 5 or more? Without doing any calculations, you probably know
that the probability is pretty high since the difference in population
means is 10. But what exactly is the probability?
First, let's determine the sampling distribution
of the difference between means. Using the formulas above, the
mean is

The standard error is:

The sampling distribution is shown in Figure 1. Notice that it
is normally distributed with a mean of 10 and a standard deviation
of 3.317. The area above 5 is shaded blue.
The last step is to determine the area that is
shaded blue. Using either a Z table or the normal
calculator, the area can be determined to be 0.934. Thus the
probability that the mean of the sample from Species 1 will exceed
the mean of the sample from Species 2 by 5 or more is 0.934.
As shown below, the formula for the standard error
of the difference between means is much simpler if the sample
sizes and the population variances are equal. When the variances
and samples sizes are the same, there is no need to use the subscripts
1 and 2 to differentiate these terms.

This simplified version of the formula can be
used for the following problem: The mean height of 15-year-old
boys (in cm) is 175 and the variance is 64. For girls, the mean
is 165 and the variance is 64. If eight boys and eight girls were
sampled, what is the probability that the mean height of the sample
of girls would be higher than the mean height of the sample of boys? In
other words, what is the probability that the mean height of girls
minus the mean height of boys is greater than 0?
As before, the problem can be solved in terms of
the sampling distribution of the difference between means (girls
- boys). The mean of the distribution is 165 - 175 = -10. The
standard deviation of the distribution is:

A graph of the distribution is shown in Figure 2.
It is clear that it is unlikely that the mean height for girls
would be higher than the mean height for boys since in the population
boys are quite a bit taller. Nonetheless it is not inconceivable
that the girls' mean could be higher than the boys' mean.
A difference between means of 0 or higher is a difference
of 10/4 = 2.5 standard deviations above the mean of -10. The probability
of a score 2.5 or more standard deviations above the mean is 0.0062.
Please answer the questions:
|