|
|
Exercises
Author(s)
David M. Lane
Prerequisites
All material presented in the Summarizing Distributions chapter
Selected answers
- Make up a dataset of 12 numbers with a positive skew. Use
a statistical program to compute the skew. Is the mean larger
than the median as it usually is for distributions with a
positive skew? What is the value for skew? (relevant
section & relevant
section )
- Repeat Problem 1 only this time make the
dataset have a negative skew. (relevant
section & relevant
section)
- Make
up three data sets with 5 numbers each that have:
(a) the same mean but different standard deviations.
(b) the same mean but different medians.
(c) the same median but different means.
(relevant section & relevant section)
- Find the mean and median for the following three variables:
(relevant section)
A B C
8 4 6
5 4 2
7 6 3
1 3 4
3 4 1
- A sample of 30 distance scores measured
in yards has a mean of 7, a variance of 16, and a standard
deviation of 4. (a) You want to convert all your distances
from yards to feet, so you multiply each score in the sample
by 3. What are the new mean, variance, and standard deviation?
(b) You then decide that you only want to look at the distance
past a certain point. Thus, after multiplying the original
scores by 3, you decide to subtract 4 feet from each of the
scores. Now what are the new mean, variance, and standard deviation?
(relevant section)
- You recorded the time in seconds it took for 8 participants to
solve a puzzle. These times appear below. However, when the data
was entered into the statistical program, the score that was supposed
to be 22.1 was entered as 21.2. You had calculated the following
measures of central tendency: the mean, the median, and the mean
trimmed 25%. Which of these measures of central tendency will change
when you correct the recording error? (relevant section & relevant section)
15.2
18.8
19.3
19.7
20.2
21.8
22.1
29.4
- For the test scores in question #6, which
measures of variability (range, standard deviation, variance)
would be changed if the 22.1 data point had been
erroneously
recorded as 21.2? (relevant section)
- You
know the minimum, the maximum, and the 25th, 50th, and 75th percentiles of a
distribution. Which of the following measures of central tendency or variability
can you determine?
(relevant section, relevant section & relevant section)
mean, median, mode, trimean, geometric mean,
range, interquartile range, variance, standard deviation
- For the numbers 1, 3, 4, 6, and 12:
- Find
the value (v) for which Σ(X-v)2 is minimized.
- Find
the value (v) for which Σ|x-v|
is minimized.
(relevant
section)
- Your younger brother comes home one day after taking
a science test. He says that someone at school told him that "60%
of the students in the class scored above the median test grade." What
is wrong with this statement? What if he said "60%
of the students scored below the mean?" (relevant
section)
- An experiment compared the ability of three groups
of participants to remember briefly-presented chess positions.
The data are shown below. The numbers represent the number
of pieces correctly remembered from three chess positions.
Compare the performance of each group. Consider spread as well
as central tendency. (relevant section, relevant section & relevant section)
Non-players |
Beginners |
Tournament players |
22.1 |
32.5 |
40.1 |
22.3 |
37.1 |
45.6 |
26.2 |
39.1 |
51.2 |
29.6 |
40.5 |
56.4 |
31.7 |
45.5 |
58.1 |
33.5 |
51.3 |
71.1 |
38.9 |
52.6 |
74.9 |
39.7 |
55.7 |
75.9 |
43.2 |
55.9 |
80.3 |
43.2 |
57.7 |
85.3 |
- True/False: A bimodal distribution has two
modes and two medians. (relevant section)
- True/False:
The best way to describe a skewed distribution is to report the
mean. (relevant section)
- True/False:
When plotted on the same graph, a distribution with a mean
of 50 and a standard deviation of 10 will look more spread
out than will a distribution with a mean of 60 and a standard
deviation of 5. (relevant section)
- Compare the mean, median, trimean in terms of their sensitivity
to extreme scores (relevant
section).
- If the mean time to respond to a stimulus is much higher
than the median time to respond, what can you say about
the shape of the distribution of response times? (relevant
section)
- A set of numbers is transformed by taking the log base 10
of each number. The mean of the transformed data is 1.65. What
is the geometric mean of the untransformed data? (relevant
section)
- Which measure of central tendency is most often used for
returns on investment?
- The histogram is in balance on the fulcrum.
What are the mean, median, and mode of the distribution (approximate
where necessary)?
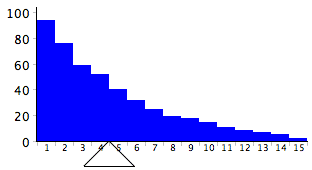
Questions from Case Studies:
The following questions are from the Angry
Moods (AM) case study.
- (AM#4) Does Anger-Out have a positive skew,
a negative skew, or no skew? (relevant
section)
- (AM#8) What is the range of the Anger-In scores?
What is the interquartile range? (relevant
section)
- (AM#12) What is the overall mean Control-Out score?
What is the mean Control-Out score for the athletes? What is
the mean Control-Out score for the non-athletes? (relevant section)
- (AM#15)
What is the variance of the Control-In scores for the athletes?
What is the variance of the Control-In scores for the non-athletes?
(relevant section)
The following question is from the Flatulence (F)
case study.
- (F#2) Based on a histogram of the variable "perday",
do you think the mean or median of this variable is larger? Calculate
the mean and median to see if you are right. (relevant
section & relevant
section)
The following questions are from the Stroop (S)
case study.
- (S#1)
Compute the mean for "words". (relevant section)
- (S#2)
Compute the mean and standard deviation for "colors".
(relevant section & relevant section)
The following questions are from the Physicians' Reactions (PR) case study.
- (PR#2) What is the mean expected time spent
for the average-weight patients? What is the mean expected
time spent for the overweight patients? (relevant section)
- (PR#3)
What is the difference in means between the groups? By approximately
how many standard deviations do the means differ?
(relevant section & relevant section)
The following question is from the Smiles
and Leniency (SL) case study.
- (SL#2) Find the mean, median, standard deviation,
and interquartile range for the leniency scores of each of
the four groups. (relevant section & relevant section)
The following questions are from the ADHD
Treatment (AT) case study.
- (AT#4) What is the mean number of correct
responses of the participants after taking the placebo (0 mg/kg)?
(relevant section)
- (AT#7)
What are the standard deviation and the interquartile range of
the d0 condition? (relevant section)
Selected Answers:
4) Variable A: Mean = 4.8, Median = 5
5) (a) Mean = 21, Var = 144, SD = 12
9) (a) 5.2
22) Non-athletes: 23.2
23) Athletes: 20.5
26) Mean = 20.2
27) Ave. weight: 31.4
29) False smile group:
Mean = 5.37
Median = 5.50
SD = 1.83
IQR = 3.0
Please answer the questions:
|
|