Summation Notation

Prerequisites
None

Learning Objectives

  1. Use summation notation to express the sum of all numbers
  2. Use summation notation to express the sum of a subset of numbers
  3. Use summation notation to express the sum of squares

Many statistical formulas involve summing numbers. Fortunately there is a convenient notation for expressing summation. This section covers the basics of this summation notation.

Let's say we have a variable X that represents the weights (in grams) of 4 grapes. The data are shown in Table 1.

Table 1. Weights of 4 grapes.
Grape
X

1
2
3
4
4.6
5.1
4.9
4.4

We label Grape 1's weight X1, Grape 2's weight X2, etc. The following formula means to sum up the weights of the four grapes:

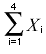
The capital Greek letter sigma (Σ) indicates summation. The "i = 1" at the bottom indicates that the summation is to start with X1 and the 4 at the top indicates that the summation will end with X4. The Xi indicates that X is the variable to be summed as i goes from 1 to 4. Therefore,

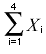= X1 + X2 + X3 + X4 = 4.6 + 5.1 + 4.9 + 4.4 = 19.0.

The symbol

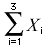
indicates that only the first 3 scores are to be summed. The index variable i goes from 1 to 3.

When all the scores of a variable (such as X) are to be summed, it is often convenient to use the following abbreviated notation:

 

Thus when no values of i are shown, it means to sum all the values of X.

Many formulas involve squaring numbers before they are summed. This is indicated as

ΣX²= 4.62 + 5.12 + 4.92 + 4.42 = 21.16 + 26.01+ 24.01 + 19.36 = 90.54

Notice that:

because the expression on the left means to sum up all the values of X and then square the sum (19² = 361) whereas the expression on the right means to square the numbers and then sum the squares (90.54, as shown).

Some formulas involve the sum of cross products. Table 2 shows the data for variables X and Y. The totals are shown in the bottom row and the cross products. are shown in the third column. The sum of the cross products. is 28.

Table 2. Sum of Cross products.
X
Y
XY
1
2
3
3
2
7
3
4
21
6
12
28

In summation notation, this is written as: ΣXY = 28.