|
One-Way Tables
Prerequisites
Chi
Square Distribution, Basic
Concepts of Probability,
Significance Testing
Learning Objectives
- Describe what it means for there to be theoretically-expected frequencies
- Compute expected frequencies
- Compute Chi Square
- Determine the degrees of freedom
The data in Table 1 were obtained by rolling a six-sided
die 36 times. If the die were a fair die, then the probability
of of any given outcome on a single roll would be 1/6.
However, as can be seen in Table 1, some outcomes occurred more
frequently than others. For example a "3" came up nine times whereas
a "4" came up only two times. Are these data consistent with the
hypothesis that the die is a fair die? Naturally, we do not expect
the sample frequencies of the six possible outcomes throws to
be the same since chance differences will occur. So, the finding
that the frequencies differ does not mean that the die is not
fair. One way to test whether the die is fair is to conduct a significance
test. The null
hypothesis is that the die is fair. This hypothesis
is tested by computing the probability of obtaining frequencies
as discrepant or more discrepant from a uniform distribution of
frequencies as obtained in the sample. If this probability is
sufficiently low, then the null hypothesis that the die is fair
can be rejected.
The first step in conducting the significance
test is to compute the expected frequency for each outcome given
that the null hypothesis is true. For example, the expected frequency
of a "1" is 6 since the probability of a "1" coming
up is 1/6 and there were a total of 36 rolls of the die.
Expected frequency = (1/6)(36) = 6
Note that the expected frequencies
are expected only in a theoretical sense. We do not really "expect"
the observed frequencies to match the "expected frequencies" exactly.
The calculation continues as follows. Letting
E be the expected frequency of an outcome and O be the observed
frequency of that outcome, compute

for each outcome. Table 2 shows these calculations.
Next we add up all the values in Column 4 of Table 2.

This sampling distribution of
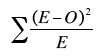
is approximately distributed as Chi Square on k-1 degrees of
freedom where k is the number of categories. Therefore, for
this problem the test statistic is

which means the value of Chi Square with 5 degrees of freedom
is 5.333.
From a Chi Square calculator it can be determined
that the probability of a Chi Square of 5.333 or larger is 0.377.
Therefore, the null hypothesis that the die is fair cannot be
rejected.
This Chi Square test can also be used to test other
deviations between expected and observed frequencies. The following
example shows a test of whether the variable "University GPA"
in the SAT and College GPA case study is normally distributed.
The second column of Table 3 shows the proportions
of a normal distribution falling between various limits. The expected
frequencies (E) are calculated by multiplying the number of scores
(105) by the proportion. The final column shows the observed number
of scores in each range. It is clear that the observed frequencies
vary greatly from the expected frequencies. Note that if the distribution
were normal then there would have been only about 35 scores between
-1 and 0 whereas 60 were observed.
The test of whether the observed scores deviate
significantly from the expected is computed using the familiar
calculation.

The subscript "3" means there are three
degrees of freedom. As before, the degrees of freedom is the number
of outcomes, which is four in this example. The Chi
Square
distribution calculator shows that p < 0.001 for this
Chi Square. Therefore, the null hypothesis that the scores are
normally distributed can be rejected.
Chi Square Calculator
|