Sampling Distribution of Difference Between Means

Prerequisites
Sampling Distributions, Sampling Distribution of the Mean, Variance Sum Law I

Learning Objectives

1. State the mean and variance of the sampling distribution of the difference between means
2. Compute the standard error of the difference between means
3. Compute the probability of a difference between means being above a specified value

Statistical analyses are very often concerned with the difference between means. A typical example is an experiment designed to compare the mean of a control group with the mean of an experimental group. Inferential statistics used in the analysis of this type of experiment depend on the sampling distribution of the difference between means.

The sampling distribution of the difference between means can be thought of as the distribution that would result if we repeated the following three steps over and over again: (1) sample n1 scores from Population 1and n2 scores from Population 2, (2) compute the means of the two samples (M1 and M2), (3) compute the difference between means M1 - M2. The distribution of the differences between means is the sampling distribution of the difference between means.

As you might expect, the mean of the sampling distribution of the mean is:

which says that the mean of the distribution of differences between sample means is equal to the difference between population means. For example, say that mean test score of all 12-year olds in a population is 34 and the mean of 10-year olds is 25. If numerous samples were taken from each age group and the mean difference computed each time, the mean of these numerous differences between sample means would be 34 - 25 = 9.

From the variance sum law, we know that:

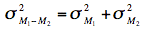
which says that the variance of the sampling distribution of the difference between means is equal to the variance of the sampling distribution of the mean for Population 1 plus the variance of the sampling distribution of the mean for Population 2. Recall the formula for the variance of the sampling distribution of the mean:

Since we have two populations and two samples sizes, we need to distinguish between the two variances and sample sizes. We do this using the subscripts 1 and 2. Using this convention we can write the formula for the variance of the sampling distribution of the difference between means as:

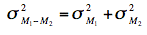
Since the standard error of a sampling distribution is the standard deviation of the sampling distribution, the standard error of the difference between means is:

Just to review the notation, the symbol on the left contains a sigma (σ) which means it is a standard deviation. The subscripts M1 - M2 indicate that it is the standard deviation of the sampling distribution of M1 - M2.

Now let's look at an application of this formula. Assume there are two species of green beings on Mars. The mean height of Species 1 is 32 while the mean height of Species 2 is 22. The variances of the two species are 60 and 70 respectively and the heights of both species are normally distributed. You randomly sample 10 members of Species 1 and 14 members of Species 2. What is the probability that the mean of the 10 members of Species 1 will exceed the mean of the 14 members of Species 2 by 5 or more? Without doing any calculations, you probably know that the probability is pretty high since the difference in population means is 10. But what exactly is the probability?

First, lets determine the sampling distribution of the difference between means. Using the formulas above, the mean is

The standard error is:

The sampling distribution is shown in Figure 1. Notice that it is normally distributed with a mean of 10 and a standard deviation of 3.317. The area above 5 is shaded blue.

Figure 1. The sampling distribution of the difference between means.

The last step is to determine the area that is shaded blue. Using either a Z table or the normal calculator, the area can be determined to be 0.934. Thus the probability that the mean of the sample from Species 2 will exceed the mean of the sample from Species 1 by 5 or more is 0.934.

As shown below, the formula for the standard error of the difference between means is much simpler if the sample sizes and the population variances are equal. Since the variances and samples sizes are the same, there is no need to use the subscripts 1 and 2 to differentiate these terms.

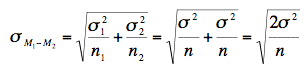
This simplified version of the formula can be used for the following problem: The mean height of 15-year olds boys (in cm) is 175 and the variance is 64. For girls, the mean is 165 and the variance is 64. If eight boys and eight girls were sampled, what is the probability that the mean height of the sample of girls would be higher than the mean height of the boys? In other words, what is the probability that the mean height of girls minus the mean height of boys is greater than 0?

As before, the problem can be solved in terms of the sampling distribution of the difference between means (girls - boys). The mean of the distribution is 165 - 175 = -10. The standard deviation of the distribution is:

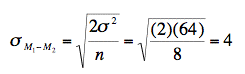
A graph of the distribution is shown in Figure 2. It is clear that it is unlikely that the mean height for girls would be higher than the mean height for boys since in the population boys are quite a bit taller. Nonetheless it is not inconceivable that the girls' mean could be higher than the boys' mean.

Figure 2. Sampling distribution of the difference between mean heights.

A difference between means of 0 or higher is a difference of 10/4 = 2.5 standard deviations above the mean of -10. The probability of a score 2.5 or more standard deviations above the mean is 0.0062.