Home

  1. Introduction
  2. Graphing Distributions
  3. Summarizing Distributions
  4. Describing Bivariate Data
  5. Probability
  6. Research Design
  7. Normal Distribution
  8. Advanced Graphs
  9. Sampling Distributions
  10. Estimation
  11. Logic of Hypothesis Testing
  12. Tests of Means
  13. Power
  14. Regression
  15. Analysis of Variance
  16. Transformations
  17. Chi Square

  18. Distribution Free Tests
    1. Contents
      Standard
    2. Benefits
      Standard         Video
    3. Randomization Tests: Two Conditions
      Standard         Video
    4. Randomization Tests: Two or More Conditions
      Standard         Video
    5. Randomization Association
      Standard         Video
    6. Fisher Exact Test
      Standard         Video
    7. Rank Randomization Two Conditions
      Standard         Video
    8. Rank Randomization Two or More Conditions
      Standard  
    9. Rank Randomization for Association
      Standard         Video
    10. Statistical Literacy
      Standard
    11. Exercises
      Standard

  19. Effect Size
  20. Case Studies
  21. Calculators
  22. Glossary
 

Rank Randomization Two or More Conditions (Kruskal-Wallis)

Author(s)

David M. Lane

Prerequisites

Randomization Test for Two or More Conditions, Wilcoxon Test, Chi Square Distribution

Learning Objectives
  1. Compute the Kruskal-Wallis test

The Kruskal-Wallis test is a rank-randomization test that extends the Wilcoxon test to designs with more than two groups. It tests for differences in central tendency in designs with one between-subjects variable. The test is based on a statistic H that is approximately distributed as Chi Square. The formula for H is shown below:

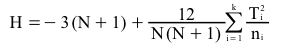
formula for Kruska-Wallis
where

N is the total number of observations,
Ti is the sum of ranks for the ith group,
ni is the sample size for the ith group,
and k is the number of groups.

The first step is to convert the data to ranks (ignoring group membership) and then find the sum of the ranks for each group. Then, compute H using the formula above. Finally, the significance test is done using a Chi Square distribution with k-1 degrees of freedom.

For the "Smiles and Leniency" case study, the sums of the ranks for the four conditions are:

False:     2732.0
Felt:      2385.5
Miserable: 2424.5
Neutral:   1776.0

Note that since there are "ties" in the data, the mean rank of the ties is used. For example, there were 10 scores of 2.5 which tied for ranks 4-13. The average of the numbers 4, 5, 6, 7, 8, 9, 10, 11, 12, and 13 is 8.5. Therefore, all values of 2.5 were assigned ranks of 8.5.

The sample size for each group is 34.

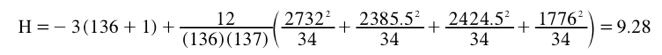
H for leniency data

Using the Chi Square Calculator for Chi Square = 9.28 with 4-1 = 3 df results in a p value of 0.0258. Thus the null hypothesis of no leniency effect can be rejected.

Please answer the questions:
correct feedback