|
|
Hypergeometric Distribution
Author(s)
David M. Lane
Prerequisites
Binomial Distribution, Permutations and Combinations
The hypergeometric distribution is used to calculate probabilities when sampling without replacement. For example, suppose you first randomly sample one card from a deck of 52. Then, without putting the card back in the deck you sample a second and then (again without replacing cards) a third. Given this sampling procedure, what is the probability that exactly two of the sampled cards will be aces (4 of the 52 cards in the deck are aces). You can calculate this probability using the following formula based on the hypergeometric distribution:
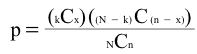 where where
k is the number of "successes" in the population
x is the number of "successes" in the sample
N is the size of the population
n is the number sampled
p is the probability of obtaining exactly x successes
kCx is the number of combinations of k things taken x at a time
In this example, k = 4 because there are four aces in the deck, x = 2 because the problem asks about the probability of getting two aces, N = 52 because there are 52 cards in a deck, and n = 3 because 3 cards were sampled. Therefore,
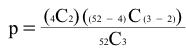 = =
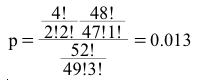
The mean and standard deviation of the hypergeometric distribution are:
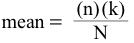

Please answer the questions:
|
|