|
|
Shapes of Distributions
Author(s)
David M. Lane
Prerequisites
Distributions,
Measures of Central Tendency, Variability
Learning Objectives
- Compute skew using two different formulas
- Compute kurtosis
We saw in the section on distributions in Chapter
1 that shapes of distributions can differ in skew
and/or kurtosis.
This section presents numerical indexes of these two measures
of shape.
Skew
Figure 1 shows a distribution with a very large
positive skew. Recall that distributions with positive skew have
tails that extend to the right.
Distributions with positive skew normally have
larger means than medians.
Just as there are several measures of central
tendency, there is more than one measure of skew. Although Pearson's
measure is a good one, the following measure is more commonly
used. It is sometimes referred to as the third moment about the
mean.
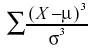
Kurtosis
The following measure of kurtosis is similar to
the definition of skew. The value "3" is subtracted
to define "no kurtosis" as the kurtosis of a normal
distribution. Otherwise, a normal distribution would have a kurtosis
of 3.
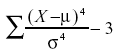
Please answer the questions:
|
|