Exercises

Author(s)

Prerequisites

You may want to use the Binomial Calculator for some of these exercises.

1. An experiment is conducted to test the claim that James Bond can taste the difference between a Martini that is shaken and one that is stirred. What is the null hypothesis? (relevant section)

2. The following explanation is incorrect. What three words should be added to make it correct? (relevant section)

The probability value is the probability of obtaining a statistic as different from the parameter specified in the null hypothesis as the statistic obtained in the experiment. The probability value is computed assuming that the null hypothesis is true.

3. Why do experimenters test hypotheses they think are false? (relevant section)

4. State the null hypothesis for:

1. An experiment testing whether echinacea decreases the length of colds.
2. A correlational study on the relationship between brain size and intelligence.
3. An investigation of whether a self-proclaimed psychic can predict the outcome of a coin flip.
4. A study comparing a drug with a placebo on the amount of pain relief. (A one-tailed test was used.)
   (relevant section & relevant section)

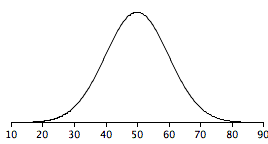
5. Assume the null hypothesis is that µ = 50 and that the graph shown below is the sampling distribution of the mean (M). Would a sample value of M= 60 be significant in a two-tailed test at the .05 level? Roughly what value of M would be needed to be significant? (relevant section & relevant section)

6. A researcher develops a new theory that predicts that vegetarians will have more of a particular vitamin in their blood than non-vegetarians. An experiment is conducted and vegetarians do have more of the vitamin, but the difference is not significant. The probability value is 0.13. Should the experimenter's confidence in the theory increase, decrease, or stay the same? (relevant section)

7. A researcher hypothesizes that the lowering in cholesterol associated with weight loss is really due to exercise. To test this, the researcher carefully controls for exercise while comparing the cholesterol levels of a group of subjects who lose weight by dieting with a control group that does not diet. The difference between groups in cholesterol is not significant. Can the researcher claim that weight loss has no effect? (relevant section)

8. A significance test is performed and p = .20. Why can't the experimenter claim that the probability that the null hypothesis is true is .20? (relevant section, relevant section & relevant section)

9. For a drug to be approved by the FDA, the drug must be shown to be safe and effective. If the drug is significantly more effective than a placebo, then the drug is deemed effective. What do you know about the effectiveness of a drug once it has been approved by the FDA (assuming that there has not been a Type I error)? (relevant section)

10. When is it valid to use a one-tailed test? What is the advantage of a one-tailed test? Give an example of a null hypothesis that would be tested by a one-tailed test. (relevant section)

11. Distinguish between probability value and significance level. (relevant section)

12. Suppose a study was conducted on the effectiveness of a class on "How to take tests." The SAT scores of an experimental group and a control group were compared. (There were 100 subjects in each group.) The mean score of the experimental group was 503 and the mean score of the control group was 499. The difference between means was found to be significant, p = .037. What do you conclude about the effectiveness of the class? (relevant section & relevant section)

13. Is it more conservative to use an alpha level of .01 or an alpha level of .05? Would beta be higher for an alpha of .05 or for an alpha of .01? (relevant section)

14. Why is "Ho: "M1 = M2" not a proper null hypothesis? (relevant section)

15. An experimenter expects an effect to come out in a certain direction. Is this sufficient basis for using a one-tailed test? Why or why not? (relevant section)

16. How do the Type I and Type II error rates of one-tailed and two-tailed tests differ? (relevant section & relevant section)

17. A two-tailed probability is .03. What is the one-tailed probability if the effect were in the specified direction? What would it be if the effect were in the other direction? (relevant section)

18. You choose an alpha level of .01 and then analyze your data. (a) What is the probability that you will make a Type I error given that the null hypothesis is true? (b) What is the probability that you will make a Type I error given that the null hypothesis is false? (relevant section)

19. Why doesn't it make sense to test the hypothesis that the sample mean is 42? (relevant section & relevant section)

20. True/false: It is easier to reject the null hypothesis if the researcher uses a smaller alpha (α) level. (relevant section & relevant section)

21. True/false: You are more likely to make a Type I error when using a small sample than when using a large sample. (relevant section)

22. True/false: You accept the alternative hypothesis when you reject the null hypothesis. (relevant section)

23. True/false: You do not accept the null hypothesis when you fail to reject it. (relevant section)

24. True/false: A researcher risks making a Type I error any time the null hypothesis is rejected. (relevant section)                        

feedback