|
|
Poisson Distribution
Author(s)
David M. Lane
Prerequisites
Logarithms
The Poisson distribution can be used to calculate the probabilities of various numbers of "successes" based on the mean number of successes. In order to apply the Poisson distribution, the various events must be independent. Keep in mind that the term "success" does not really mean success in the traditional positive sense. It just means that the outcome in question occurs.
Suppose you knew that the mean number of calls to a fire station on a weekday is 8. What is the probability that on a given weekday there would be 11 calls? This problem can be solved using the following formula based on the Poisson distribution:
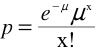 where where
e is the base of natural logarithms (2.7183)
μ
is the mean number of "successes"
x is the number of "successes" in question
For this example,
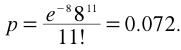
since the mean is 8 and the question pertains to 11 fires.
The mean of the Poisson distribution is μ. The variance is also equal to μ. Thus, for this example, both the mean and the variance are equal to 8.
Please answer the questions:
|
|