Multinomial Distribution

Author(s)

Prerequisites

1. Define multinomial outcomes
2. Compute probabilities using the multinomial distribution

The binomial distribution allows one to compute the probability of obtaining a given number of binary outcomes. For example, it can be used to compute the probability of getting 6 heads out of 10 coin flips. The flip of a coin is a binary outcome because it has only two possible outcomes: heads and tails. The multinomial distribution can be used to compute the probabilities in situations in which there are more than two possible outcomes. For example, suppose that two chess players had played numerous games and it was determined that the probability that Player A would win is 0.40, the probability that Player B would win is 0.35, and the probability that the game would end in a draw is 0.25. The multinomial distribution can be used to answer questions such as: "If these two chess players played 12 games, what is the probability that Player A would win 7 games, Player B would win 2 games, and the remaining 3 games would be drawn?" The following formula gives the probability of obtaining a specific set of outcomes when there are three possible outcomes for each event:

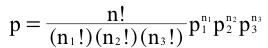
where

p is the probability,
n is the total number of events
n₁ is the number of times Outcome 1 occurs,
n₂ is the number of times Outcome 2 occurs,
n₃ is the number of times Outcome 3 occurs,
p₁ is the probability of Outcome 1
p₂ is the probability of Outcome 2, and
p₃ is the probability of Outcome 3.

For the chess example,

n = 12 (12 games are played),
n₁ = 7 (number won by Player A),
n₂ = 2 (number won by Player B),
n₃ = 3 (the number drawn),
p₁ = 0.40 (probability Player A wins)
p₂ = 0.35(probability Player B wins)
p₃ = 0.25(probability of a draw)

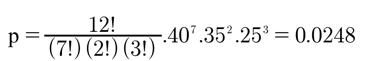
The formula for k outcomes is

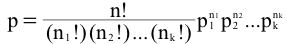
Note that the binomial distribution is a special case of the multinomial when k = 2.

feedback