Specific Comparisons (Independent Groups)

Author(s)

Prerequisites

1. Define linear combination
2. Specify a linear combination in terms of coefficients
3. Do a significance test for a specific comparison

There are many situations in which the comparisons among means are more complicated than simply comparing one mean with another. This section shows how to test these more complex comparisons. The methods in this section assume that the comparison among means was decided on before looking at the data. Therefore these comparisons are called planned comparisons. A different procedure is necessary for unplanned comparisons.

Let's begin with the made-up data from a hypothetical experiment shown in Table 1. Twelve subjects were selected from a population of high-self-esteem subjects (esteem = 1) and an additional 12 subjects were selected from a population of low-self-esteem subjects (esteem = 2). Subjects then performed on a task and (independent of how well they really did) half in each esteem category were told they succeeded (outcome = 1) and the other half were told they failed (outcome = 2). Therefore, there were six subjects in each of the four esteem/outcome combinations and 24 subjects in all.

After the task, subjects were asked to rate (on a 10-point scale) how much of their outcome (success or failure) they attributed to themselves as opposed to being due to the nature of the task.

The means of the four conditions are shown in Table 2.

There are several questions we can ask about the data. We begin by asking whether, on average, subjects who were told they succeeded differed significantly from subjects who were told they failed. The means for subjects in the success condition are 7.333 for the high-self-esteem subjects and 5.500 for the low-self-esteem subjects. Therefore, the mean for all subjects in the success condition is (7.3333 + 5.5000)/2 = 6.4167. Similarly, the mean for all subjects in the failure condition is (4.8333 + 7.8333)/2 = 6.3333. The question is: How do we do a significance test for this difference of 6.4167-6.3333 = 0.083?

The first step is to express this difference in terms of a linear combination using a set of coefficients and the means. This may sound complex, but it is really pretty easy. We can compute the mean of the success conditions by multiplying each success mean by 0.5 and then adding the result. In other words, we compute

(.5)(7.333) + (.5)(5.500)
= 3.67 + 2.75
= 6.42

Similarly, we can compute the mean of the failure conditions by multiplying each "failure" mean by 0.5 and then adding the result:

(.5)(4.833) + (.5)(7.833)
= 2.417 + 3.917
= 6.33

The difference between the two means can be expressed as

.5 x 7.333 + .5 x 5.500 -(.5 x 4.833 + .5 x 7.833) =
.5 x 7.333 + .5 x 5.500 - .5 x 4.833 - .5 x 7.833

We therefore can compute the difference between the "success" mean and the "failure" mean by multiplying each "success" mean by 0.5, each failure mean by -0.5, and adding the results. In Table 3, the coefficient column is the multiplier and the product column is the result of the multiplication. If we add up the four values in the product column, we get

L = 3.667 + 2.750 - 2.417 - 3.917 = 0.083.

This is the same value we got when we computed the difference between means previously (within rounding error). We call the value "L" for "linear combination."

Now, the question is whether our value of L is significantly different from 0. The general formula for L is

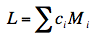
where ci is the ith coefficient and Mi is the ith mean. As shown above, L = 0.083. The formula for testing L for significance is shown below:

In this example,

MSE is the mean of the variances. The four variances are shown in Table 4. Their mean is 1.625. Therefore MSE = 1.625.

The value of n is the number of subjects in each group. Here n = 6.

Putting it all together,

We need to know the degrees of freedom in order to compute the probability value. The degrees of freedom is

df = N - k

where N is the total number of subjects (24) and k is the number of groups (4). Therefore, df = 20. Using the Online Calculator, we find that the two-tailed probability value is 0.874. Therefore, the difference between the "success" condition and the "failure" condition is not significant.

Online Calculator: t distribution

A more interesting question about the results is whether the effect of outcome (success or failure) differs depending on the self-esteem of the subject. For example, success may make high-self-esteem subjects more likely to attribute the outcome to themselves, whereas success may make low-self-esteem subjects less likely to attribute the outcome to themselves.

To test this, we have to test a difference between differences. Specifically, is the difference between success and failure outcomes for the high-self-esteem subjects different from the difference between success and failure outcomes for the low-self-esteem subjects? The means shown in Table 5 show that this is the case. For the high-self-esteem subjects, the difference between the success and failure attribution scores is 7.333-4.833 = 2.500. For low-self-esteem subjects, the difference is 5.500-7.833 = -2.333. The difference between differences is 2.500 - (-2.333) = 4.833.

The coefficients to test this difference between differences are shown in Table 5.

If it is hard to see where these coefficients came from, consider that our difference between differences was computed this way:

(7.33 - 4.83) - (5.50 - 7.83)

= 7.33 - 4.83 - 5.50 + 7.83

= (1)7.33 + (-1)4.83 + (-1)5.50 + (1)7.83

The values in parentheses are the coefficients.

To continue the calculations,

The two-tailed p value is 0.0002. Therefore, the difference between differences is highly significant.

In a later chapter on Analysis of Variance, you will see that comparisons such as this are testing what is called an interaction. In general, there is an interaction when the effect of one variable differs as a function of the level of another variable. In this example, the effect of the outcome variable is different depending on the subject's self-esteem. For the high-self-esteem subjects, success led to more self-attribution than did failure; for the low-self-esteem subjects, success led to less self-attribution than did failure.

Multiple Comparisons

The more comparisons you make, the greater your chance of a Type I error. It is useful to distinguish between two error rates: (1) the per-comparison error rate and (2) the familywise error rate. The per-comparison error rate is the probability of a Type I error for a particular comparison. The familywise error rate is the probability of making one or more Type I errors in a family or set of comparisons. In the attribution experiment discussed above, we computed two comparisons. If we use the 0.05 level for each comparison, then the per-comparison rate is simply 0.05. The familywise rate can be complex. Fortunately, there is a simple approximation that is fairly accurate when the number of comparisons is small. Defining α as the per-comparison error rate and c as the number of comparisons, the following inequality always holds true for the familywise error rate (FW):

FW ≤ cα

This inequality is called the Bonferroni inequality. In practice, FW can be approximated by cα. This is a conservative approximation since FW can never be greater than cα and is generally less than cα.

The Bonferroni inequality can be used to control the familywise error rate as follows: If you want the familywise error rate to be α, you use α/c as the per-comparison error rate. This correction, called the Bonferroni correction, will generally result in a familywise error rate less than α. Alternatively, you could multiply the probability value by c and use the original α level.

Should the familywise error rate be controlled? Unfortunately, there is no clear-cut answer to this question. The disadvantage of controlling the familywise error rate is that it makes it more difficult to obtain a significant result for any given comparison: The more comparisons you do, the lower the per-comparison rate must be and therefore the harder it is to reach significance. That is, the power is lower when you control the familywise error rate. The advantage is that you have a lower chance of making a Type I error.

One consideration is the definition of a family of comparisons. Let's say you conducted a study in which you were interested in whether there was a difference between male and female babies in the age at which they started crawling. After you finished analyzing the data, a colleague of yours had a totally different research question: Do babies who are born in the winter differ from those born in the summer in the age they start crawling? Should the familywise rate be controlled or should it be allowed to be greater than 0.05? Our view is that there is no reason you should be penalized (by lower power) just because your colleague used the same data to address a different research question. Therefore, the familywise error rate need not be controlled. Consider the two comparisons done on the attribution example at the beginning of this section: These comparisons are testing completely different hypotheses. Therefore, controlling the familywise rate is not necessary.

Now consider a study designed to investigate the relationship between various variables and the ability of subjects to predict the outcome of a coin flip. One comparison is between males and females; a second comparison is between those over 40 and those under 40; a third is between vegetarians and non-vegetarians; and a fourth is between firstborns and others. The question of whether these four comparisons are testing different hypotheses depends on your point of view. On the one hand, there is nothing about whether age makes a difference that is related to whether diet makes a difference. In that sense, the comparisons are addressing different hypotheses. On the other hand, the whole series of comparisons could be seen as addressing the general question of whether anything affects the ability to predict the outcome of a coin flip. If nothing does, then allowing the familywise rate to be high means that there is a high probability of reaching the wrong conclusion.

Orthogonal Comparisons

In the preceding sections, we talked about comparisons being independent. Independent comparisons are often called orthogonal comparisons. There is a simple test to determine whether two comparisons are orthogonal: If the sum of the products of the coefficients is 0, then the comparisons are orthogonal. Consider again the experiment on the attribution of success or failure. Table 6 shows the coefficients previously presented in Table 3 and in Table 5. The column "C1" contains the coefficients from the comparison shown in Table 3; the column "C2" contains the coefficients from the comparison shown in Table 5. The column labeled "Product" is the product of these two columns. Note that the sum of the numbers in this column is 0. Therefore, the two comparisons are orthogonal.

Table 7 shows two comparisons that are not orthogonal. The first compares the high-self-esteem subjects to low-self-esteem subjects; the second considers only those in the success group and compares high-self-esteem subjects to low-self-esteem subjects. The failure group is ignored by using 0's as coefficients. Clearly the comparison of these two groups of subjects for the whole sample is not independent of the comparison of them for the success group only. You can see that the sum of the products of the coefficients is 0.5 and not 0.

feedback