|
Difference between Two Means (Independent
Groups)
Author(s)
David M. Lane
Prerequisites
Sampling
Distribution of Difference between Means, Confidence
Intervals, Confidence
Interval on the Difference between Means, Logic
of Hypothesis Testing,
Testing a Single Mean
Learning Objectives
- State the assumptions for testing the difference between two means
- Estimate the population variance assuming homogeneity of variance
- Compute the standard error of the difference between means
- Compute t and p for the difference between means
- Format data for computer analysis
It is much more common for a researcher to be
interested in the difference between means than in the specific
values of the means themselves. This section covers how to test
for differences between means from two separate groups of subjects.
A later section describes how
to test for differences between the means of two conditions
in designs where only one group of subjects is used and each
subject is tested in each condition.
We take as an example the data from the "Animal
Research" case study. In this experiment, students rated
(on a 7-point scale) whether they thought animal research is wrong.
The sample sizes, means, and variances are shown separately for
males and females in Table 1.
Table 1. Means and Variances in Animal Research study.
|
Group
|
n
|
Mean
|
Variance
|
|
Females
|
17
|
5.353
|
2.743
|
|
Males
|
17
|
3.882
|
2.985
|
As you can see, the females rated animal research
as more wrong than did the males. This sample difference between
the female mean of 5.35 and the male mean of 3.88 is 1.47. However,
the gender difference in this particular sample is not very
important. What is important is whether there is a difference
in the population means.
In order to test whether there is a difference
between population means, we are going to make three assumptions:
- The two populations have the same variance. This assumption
is called the assumption of homogeneity of
variance.
- The populations are normally
distributed.
- Each value is sampled independently from
each other value. This assumption requires that each subject
provide only one value. If a subject provides two scores,
then the scores are not independent. The analysis of data
with two scores per subject is shown in the section on the correlated
t test later in this chapter.
The consequences of violating the first two
assumptions are investigated in the simulation
in the next section. For now, suffice it to say that small-to-moderate
violations of assumptions 1 and 2 do not make much difference.
It is important not to violate assumption 3.
We saw the following general formula for significance
testing in the section on testing a
single mean:

In this case, our statistic is the difference between
sample means and our hypothesized value is 0. The hypothesized
value is the null hypothesis that the difference between population
means is 0.
We continue to use the data from the "Animal
Research" case study and will compute a significance test
on the difference between the mean score of the females and the
mean score of the males. For this calculation, we will make
the three assumptions specified above.
The first step is to compute the statistic, which
is simply the difference between means.
M1 - M2
= 5.3529 - 3.8824 = 1.4705
Since the hypothesized value is 0, we do not need
to subtract it from the statistic.
The next step is to compute the estimate of the
standard error of the statistic. In this case, the statistic is
the difference between means, so the estimated standard error of
the statistic is (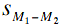 ).
Recall from the relevant
section in the chapter on sampling distributions that the
formula for the standard error of the difference between means is: ).
Recall from the relevant
section in the chapter on sampling distributions that the
formula for the standard error of the difference between means is:

In order to estimate this quantity, we estimate
σ2 and use that estimate in place
of σ2. Since we are assuming the
two population variances are the same, we estimate this variance by
averaging our two sample variances. Thus, our estimate of variance
is computed using the following formula:

where MSE is our estimate of σ2.
In this example,
MSE = (2.743 + 2.985)/2 = 2.864.
Since n (the number of scores in
each group) is 17,
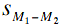 = = = = = 0.5805.
= 0.5805.
The next step is to compute t by plugging these
values into the formula:
t = 1.4705/.5805 = 2.533.
Finally, we compute the probability of getting
a t as large or larger than 2.533 or as small or smaller than
-2.533. To do this,
we need to know the degrees
of freedom. The degrees of freedom is the number
of independent estimates of variance on which MSE is based.
This is equal to (n1 - 1) + (n2
- 1), where n1 is the sample size of
the first group and n2 is the sample
size of the second group. For this example, n1 = n2 = 17. When n1 = n2, it is conventional to use "n"
to refer to the sample size of each group. Therefore, the degrees
of freedom is 16 + 16 = 32.
Once we have the degrees of freedom, we can use
the t distribution calculator to find the probability. Figure
1 shows that the probability value for a two-tailed test is 0.0164.
The two-tailed test is used when the null hypothesis can be rejected
regardless of the direction of the effect. As shown in Figure
1, it is the probability of a t < -2.533 or
a t > 2.533.
The results of a one-tailed test are shown in
Figure 2. As you can see, the probability value of 0.0082 is half
the value for the two-tailed test.
Online
Calculator: t distribution
Formatting Data for Computer Analysis
Most computer programs that compute t tests require
your data to be in a specific form. Consider the data in Table
2.
Table 2. Example Data.
|
Group 1
|
Group 2
|
|
3
|
2
|
|
4
|
6
|
|
5
|
8
|
Here there are two groups, each with three observations. To format
these data for a computer program, you normally have to use two
variables: the first specifies the group the subject is in and
the second is the score itself. The reformatted version of the data in Table 2 is shown in Table 3.
Table 3. Reformatted Data.
|
G
|
Y
|
|
1
|
3
|
|
1
|
4
|
|
1
|
5
|
|
2
|
2
|
|
2
|
6
|
|
2
|
8
|
To use Analysis
Lab to do the calculations, you would copy the data and then
- Click the "Enter/Edit Data" button. (You may
be warned that for security reasons you must use the keyboard
shortcut for pasting data.)
- Paste your data.
- Click "Accept Data."
- Set the Dependent Variable to Y.
- Set the Grouping Variable to G.
- Click the "t-test/confidence interval" button.
The t value is -0.718, the df = 4, and p = 0.512.
Computations for Unequal Sample Sizes (optional)
The calculations are somewhat more
complicated when the sample sizes are not equal. One consideration
is that MSE, the estimate of variance, counts the group with
the larger sample size more than the group with the smaller
sample size. Computationally, this is done by computing the sum
of squares error (SSE) as follows:

where M1 is the mean for group 1 and
M2 is the mean for group 2. Consider
the following small example:
Table 4. Unequal n.
|
Group 1
|
Group 2
|
|
3
|
2
|
|
4
|
4
|
|
5
|
|
M1 = 4 and M2 = 3.
SSE = (3-4)2 + (4-4)2 +
(5-4)2 + (2-3)2 +
(4-3)2 = 4
Then, MSE is computed by: MSE = SSE/df
where the degrees of freedom (df) is computed as before:
df = (n1 - 1) + (n2 - 1) = (3 - 1) + (2 - 1) = 3.
MSE = SSE/df = 4/3 = 1.333.
The formula
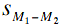 = =
is replaced by
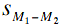 = =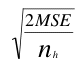
where nh is the harmonic mean of the sample sizes and is computed
as follows:
nh = 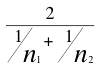 = =
 = 2.4.
= 2.4.
and
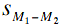 = =
 = 1.054.
= 1.054.
Therefore,
t = (4-3)/1.054 = 0.949
and the two-tailed p = 0.413.
Data file
data=read.csv(file="animal.csv")
t.test(data$WRONG ~ data$GENDER,var.equal=TRUE)
Two Sample t-test
data: data$WRONG by data$GENDER
t = 2.5335, df = 32, p-value = 0.01639
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
0.2882231 2.6529534
sample estimates:
mean in group 1 mean in group 2
5.352941 3.882353
Please answer the questions:
|