Differences between Two Means (Independent Groups)

Prerequisites
Sampling Distribution of Difference between Means, Confidence Intervals, Confidence Interval on the Difference between Means, Logic of Hypothesis Testing, Testing a Single Mean

Learning Objectives

  1. State the assumptions for testing the difference between two means
  2. Estimate the population variance assuming homogeneity of variance
  3. Compute the standard error of the difference between means
  4. Compute t and p for the difference between means.

It is much more common for a researcher to be interested in the difference between means than in the specific values of the means themselves. This section covers how to test for differences between means from two separate groups of subjects. A later section describes how to test for differences between the means of two conditions in designs where only one group of subjects is used and each subject is tested in each condition.

We take as an example the data from the "Animal Research " case study. In this experiment, students rated (on a 7-point scale) whether they thought animal research is wrong. The sample sizes, means, and variances are shown separately for males and females in Table 1.

Table 1. Means and Variances in Animal Research study.
Condition n Mean Variance
Females
Males		 17
17		 5.353
3.882		 2.743
2.985

As you can see, the females rated animal research as more wrong than did the males. This sample difference between the female mean of 5.35 and the male mean of 3.88 is 1.47. However, the gender difference in this particular sample is not very important. What is important is whether there is a difference in the population means.

In order to test whether there is a difference between population means, we are going to make three assumptions:

    1. The two populations have the same variance. This assumption is called the assumption of homogeneity of variance.
    2. The populations are normally distributed.
    3. Each value is sampled independently from each other value. This assumption requires that each subject provide only one value. If a subject provides two scores, then the scores are not independent. The analysis of data with two scores per subject is shown in the section on the correlated t test later in this chapter.

The consequences of violating the former two assumptions are investigated in the simulation in the next section. For now, suffice it to say that small-to-moderate violations of assumptions 1 and 2 do not make much difference. It is important not to violate assumption 3.

We saw the following general formula for significance testing in the section on testing a single mean:

In this case, our statistic is the difference between sample means and our hypothesized value is 0. The hypothesized value is the null hypothesis that the difference between population means is 0.

We continue to use the data from the "Animal Research" case study and will compute a significance test on the difference between the mean score of the males and the mean score of the females. For this calculation, we will make the three assumptions specified above.

The first step is to compute the statistic, which is simply the difference between means.

M1 - M2 = 5.3523 - 3.8824 = 1.470

Since the hypothesized value is 0, we do not need to subtract it from the statistic.

The next step is to compute the estimate of the standard error of the statistic. In this case, the statistic is the difference between means so the estimated standard error of the statistic is (). Recall from the relevant section in the chapter on sampling distributions that the formula for the standard error of the difference in means in the population is:


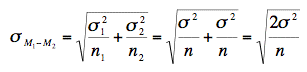
In order to estimate this quantity, we estimate σ2 and use that estimate in place of σ2. Since we are assuming the population variances are the same, we estimate this variance by averaging our two sample variances. Thus, our estimate of variance is computed using the following formula:

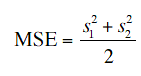
where MSE is our estimate of σ2. In this example,

MSE = (2.743 + 2.985)/2 = 2.864.

Since n (the number of scores in each condition) is 17,

== = 0.5805.

The next step is to compute t by plugging these values into the formula:

t = 1.47/.5805 = 2.533.

Finally, we compute the probability of getting a t as large or larger than 2.53 or as small or smaller than -2.53. To do this, we need to know the degrees of freedom. The degrees of freedom is the number of independent estimates of variance on which MSE is based. This is equal to (n1 -1) + (n2 -1) where n1 is the sample size for the first group and n2 is the sample size of the second group. For this example, n1= n2 = 17. When n1= n2, it is conventional to use "n" to refer to the sample size of each group. Therefore the degrees for freedom is 16 + 16 = 32.

Once we have the degrees of freedom, we can use the t distribution calculator to find the probability. Figure 1 shows that the probability value for a two-tailed test is 0.0164. The two-tailed test is used when the null hypothesis can be rejected regardless of the direction of the effect. As shown in Figure 1, it is the probability of a t < -2.533 or > 2.533.

Figure 1. The two-tailed probability.

The results of a one-tailed test are shown in Figure 2. As you can see, the probability value of 0.0082 is half the value for the two-tailed test.

Figure 2. The two-tailed probability.

 

Online Calculator: t distribution

Formatting data for Computer Analysis

Most computer programs that compute t tests require your data be in a specific form. Consider the data in Table 2.

Table 2. Example Data
Group 1 Group 2

3
4
5

2
4
6

Here there are two groups, each with three observations. To format these data for a computer program, you normally have to use two variables: the first specifies the group the subject is in and the second is the score itself. For the data in Table 2, the reformatted data look as follows.

Table 3. Reformatted
Data

G Y
1 3
1 4
1 5
2 2
2 4
2 6

To use Analysis Lab to do the calculations, you would copy the data and then

  1. Click the "Enter/Edit User Data" button (You may be warned that for security reasons you must use the keyboard shortcut for pasting data).
  2. Paste your data.
  3. Click "Accept Data"
  4. Set the Dependent Variable to Y
  5. Set the Grouping Variable to G
  6. Click the t-test confidence interval button.

The t value is -2.4495, the df = 4, and p = 0.0705.

Computations for Unequal Sample Sizes (optional)

The calculations are somewhat more complicated when the sample sizes are not equal. One consideration is that MSE, the estimate of variance, counts the sample with the larger sample size more than the sample with the smaller sample size. Computationally this is done by computing the sum of squares error (SSE) as follows:



where M1 is the mean for group 1 and M2 is the mean for group 2. Consider the following small example:

Table 4. Unequal n
Group 1 Group 2

3
4
5

2
4

M1 = 4 and M2 = 3.

SSE = (3-4)2 + (4-4)2 + (5-4)2 + (2-3)2 + (4-3)2 = 4

Then, MSE is computed by: MSE = SSE/df

where the degrees of freedom (df) are computed as before:
df = (n1 -1) + (n2 -1) = (3-1) + (2-1) = 3.
MSE = SSE/df = 4/3 = 1.333.

The formula

=

is replaced by

=

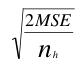
where nh is the harmonic mean of the sample sizes and is computed as follows:

nh = 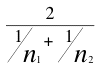= = 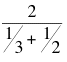2.4.
and

= = 1.054.


Therefore,

t = (4-3)/1.054 = 0.949

and the two-tailed p = 0.413.