|
|
Computing Pearson's r
Author(s)
David M. Lane
Prerequisites
Summation
Notation, Introduction to Bivariate Data
Learning Objectives
- Define X and x
- State why Σxy = 0 when there is no relationship
- Calculate r
There are several formulas that can be used to
compute Pearson's correlation. Some formulas make more conceptual
sense whereas others are easier to actually compute. We are
going to begin with a formula that makes more conceptual sense.
We are going to compute the correlation between
the variables X and Y shown in Table 1. We begin by computing
the mean for X and subtracting this mean from all values of
X. The new variable is called "x." The variable "y"
is computed similarly. The variables x and y are said to be deviation
scores because each score is a deviation from the mean.
Notice that the means of x and y are both 0. Next we create
a new column by multiplying x and y.
Before proceeding with the calculations, let's
consider why the sum of the xy column reveals the relationship
between X and Y. If there were no relationship between X and
Y, then positive values of x would be just as likely to be paired
with negative values of y as with positive values. This would
make negative values of xy as likely as positive values and
the sum would be small. On the other hand, consider Table 1
in which high values of X are associated with high values of
Y and low values of X are associated with low values of Y. You
can see that positive values of x are associated with positive
values of y and negative values of x are associated with negative
values of y. In all cases, the product of x and y is positive,
resulting in a high total for the xy column. Finally, if there
were a negative relationship then positive values of x would
be associated with negative values of y and negative values
of x would be associated with positive values of y. This would
lead to negative values for xy.
Table 1. Calculation of r.
| |
X |
Y |
x |
y |
xy |
x2 |
y2 |
| |
1 |
4 |
-3 |
-5 |
15 |
9 |
25 |
| |
3 |
6 |
-1 |
-3 |
3 |
1 |
9 |
| |
5 |
10 |
1 |
1 |
1 |
1 |
1 |
| |
5 |
12 |
1 |
3 |
3 |
1 |
9 |
| |
6 |
13 |
2 |
4 |
8 |
4 |
16 |
| Total |
20 |
45 |
0 |
0 |
30 |
16 |
60 |
| Mean |
4 |
9 |
0 |
0 |
6 |
|
|
Pearson's r is designed so that the correlation
between height and weight is the same whether height is measured
in inches or in feet. To achieve this property, Pearson's correlation
is computed by dividing the sum of the xy column (Σxy)
by the square root of the product of the sum of the x2 column
(Σx2) and
the sum of the y2 column (Σy2).
The resulting formula is:
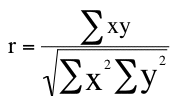
and therefore
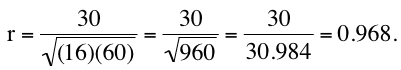
An alternative computational formula that avoids
the step of computing deviation scores is:
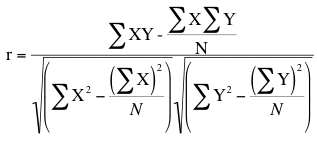
Please answer the questions:
|
|