|
Summation Notation
Author(s)
David M. Lane
Prerequisites
None
Learning Objectives
- Use summation notation to express the sum of all numbers
- Use summation notation to express the sum of a subset of numbers
- Use summation notation to express the sum of squares
Many statistical formulas involve summing numbers.
Fortunately there is a convenient notation for expressing summation.
This section covers the basics of this summation
notation.
Let's say we have a variable X that represents the
weights (in grams) of 4 grapes. The data are shown in Table 1.
Table 1. Weights of 4 grapes.
| Grape |
X |
1
2
3
4
|
4.6
5.1
4.9
4.4 |
We label Grape 1's weight X1,
Grape 2's weight X2, etc. The following
formula means to sum up the weights of the four grapes:

The Greek letter capital sigma (Σ)
indicates summation. The "i = 1" at the bottom indicates
that the summation is to start with X1
and the 4 at the top indicates that the summation will end with
X4. The "Xi" indicates
that X is the variable to be summed as i goes from 1 to 4. Therefore,
 = X1 + X2 +
X3 + X4 = 4.6
+ 5.1 + 4.9 + 4.4 = 19.0.
= X1 + X2 +
X3 + X4 = 4.6
+ 5.1 + 4.9 + 4.4 = 19.0.
The symbol
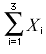
indicates that only the first 3 scores are to
be summed. The index variable i goes from 1 to 3.
When all the scores of a variable (such as X)
are to be summed, it is often convenient to use the following
abbreviated notation:

Thus, when no values of i are shown, it means to
sum all the values of X.
Many formulas involve squaring numbers before they
are summed. This is indicated as
ΣX² =
4.62 + 5.12
+ 4.92 + 4.42
= 21.16 + 26.01 + 24.01 + 19.36 = 90.54.
Notice that:

because the expression on the left means to sum up all the values
of X and then square the sum (19² = 361),
whereas the expression on the right means to square the numbers
and then sum the squares (90.54, as shown).
Some formulas involve the sum of cross products.
Table 2 shows the data for variables X and Y. The cross products (XY) are shown in the third
column. The sum of the cross products is 3 + 4 + 21 = 28.
Table 2. Cross Products.
| X |
Y |
XY |
1
2
3 |
3
2
7 |
3
4
21 |
In summation notation, this is written as: ΣXY
= 28.
Please answer the questions:
|