SPSS output

Descriptive

Descriptive statistics

How to do this

N

Range

Minimum

Maximum

Mean

Std. Deviation

Variance

ACTIVE

Statistic

Statistic

Statistic

Statistic

Statistic

Std. Error

Statistic

Statistic

1.00

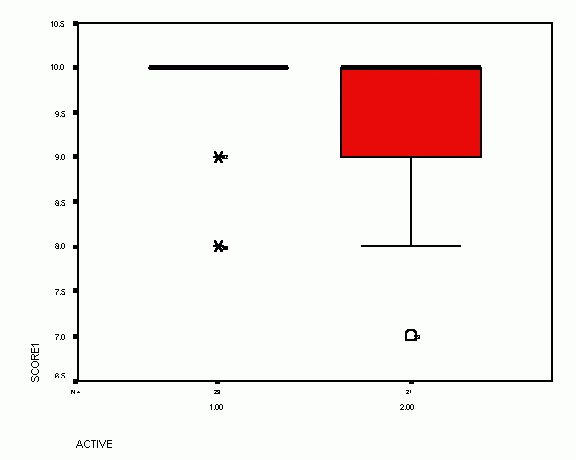
SCORE1

29

2.00

8.00

10.00

9.6207

.1351

.7277

.530

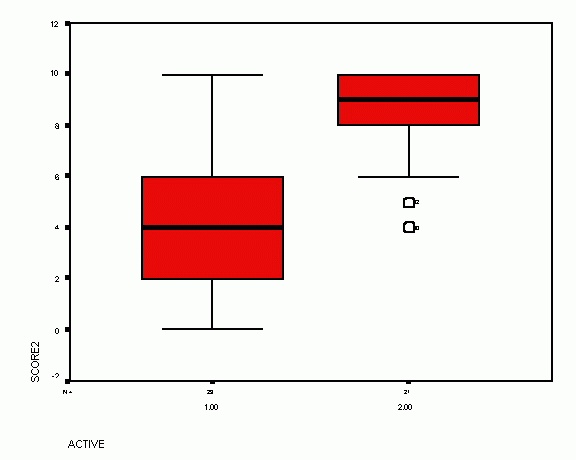
SCORE2

29

10.00

.00

10.00

4.3793

.5839

3.1443

9.887

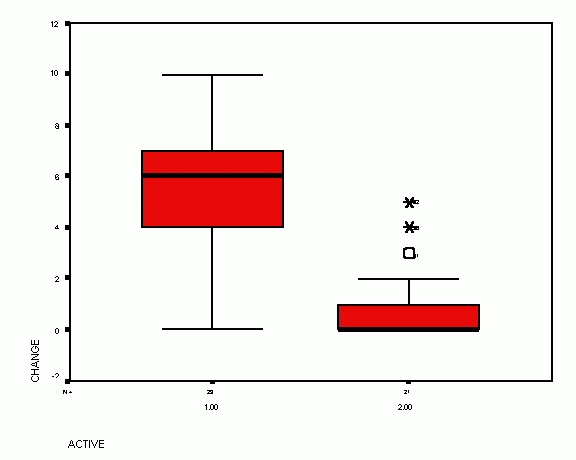
CHANGE

29

10.00

.00

10.00

5.2414

.6010

3.2366

10.475

Valid N (listwise)

29








2.00

SCORE1

21

3.00

7.00

10.00

9.5238

.1905

.8729

.762

SCORE2

21

6.00

4.00

10.00

8.4286

.4057

1.8593

3.457

CHANGE

21

5.00

.00

5.00

1.0952

.3444

1.5781

2.490

Valid N (listwise)

21








 

 

Detailed Descriptive Statistics

How to do this

ACTIVE

Cases

Valid

Missing

Total


ACTIVE

N

Percent

N

Percent

N

Percent

SCORE1

1.00

29

100.0%

0

.0%

29

100.0%

2.00

21

100.0%

0

.0%

21

100.0%

SCORE2

1.00

29

100.0%

0

.0%

29

100.0%

2.00

21

100.0%

0

.0%

21

100.0%

CHANGE

1.00

29

100.0%

0

.0%

29

100.0%

2.00

21

100.0%

0

.0%

21

100.0%


ACTIVE

Statistic

Std. Error

SCORE1

1.00

Mean

9.6207

.1351

95% Confidence Interval for Mean

Lower Bound

9.3439


Upper Bound

9.8975


5% Trimmed Mean

9.6897


Median

10.0000


Variance

.530


Std. Deviation

.7277


Minimum

8.00


Maximum

10.00


Range

2.00


Interquartile Range

.5000


Skewness

-1.647

.434

Kurtosis

1.147

.845

2.00

Mean

9.5238

.1905

95% Confidence Interval for Mean

Lower Bound

9.1265


Upper Bound

9.9211


5% Trimmed Mean

9.6349


Median

10.0000


Variance

.762


Std. Deviation

.8729


Minimum

7.00


Maximum

10.00


Range

3.00


Interquartile Range

1.0000


Skewness

-1.825

.501

Kurtosis

2.583

.972

SCORE2

1.00

Mean

4.3793

.5839

95% Confidence Interval for Mean

Lower Bound

3.1833


Upper Bound

5.5753


5% Trimmed Mean

4.3103


Median

4.0000


Variance

9.887


Std. Deviation

3.1443


Minimum

.00


Maximum

10.00


Range

10.00


Interquartile Range

4.5000


Skewness

.541

.434

Kurtosis

-.546

.845

2.00

Mean

8.4286

.4057

95% Confidence Interval for Mean

Lower Bound

7.5822


Upper Bound

9.2749


5% Trimmed Mean

8.5847


Median

9.0000


Variance

3.457


Std. Deviation

1.8593


Minimum

4.00


Maximum

10.00


Range

6.00


Interquartile Range

2.5000


Skewness

-1.062

.501

Kurtosis

.175

.972

CHANGE

1.00

Mean

5.2414

.6010

95% Confidence Interval for Mean

Lower Bound

4.0103


Upper Bound

6.4725


5% Trimmed Mean

5.2682


Median

6.0000


Variance

10.475


Std. Deviation

3.2366


Minimum

.00


Maximum

10.00


Range

10.00


Interquartile Range

5.0000


Skewness

-.335

.434

Kurtosis

-.829

.845

2.00

Mean

1.0952

.3444

95% Confidence Interval for Mean

Lower Bound

.3769


Upper Bound

1.8136


5% Trimmed Mean

.9418


Median

.0000


Variance

2.490


Std. Deviation

1.5781


Minimum

.00


Maximum

5.00


Range

5.00


Interquartile Range

1.5000


Skewness

1.431

.501

Kurtosis

.896

.972

 

 

Explore

How to do this:

 

ACTIVE

Cases

Valid

Missing

Total


ACTIVE

N

Percent

N

Percent

N

Percent

SCORE1

1.00

29

100.0%

0

.0%

29

100.0%

2.00

21

100.0%

0

.0%

21

100.0%

SCORE1

Boxplot

Explore

How to do this:

 

ACTIVE

Cases

Valid

Missing

Total


ACTIVE

N

Percent

N

Percent

N

Percent

SCORE2

1.00

29

100.0%

0

.0%

29

100.0%

2.00

21

100.0%

0

.0%

21

100.0%

SCORE2

Boxplot

Explore

How to do this:

ACTIVE

Cases

Valid

Missing

Total


ACTIVE

N

Percent

N

Percent

N

Percent

CHANGE

1.00

29

100.0%

0

.0%

29

100.0%

2.00

21

100.0%

0

.0%

21

100.0%

CHANGE

Boxplot

PPlot

How to do this:

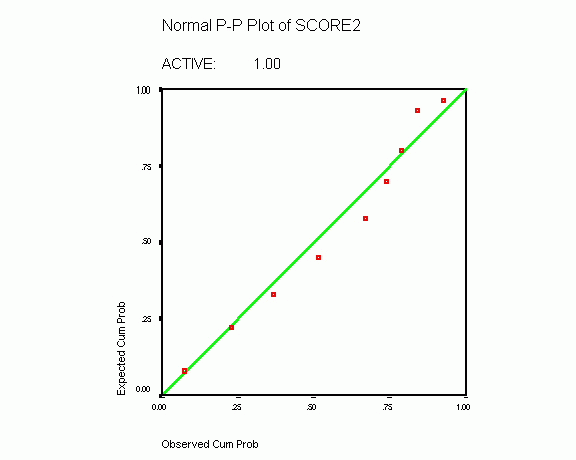
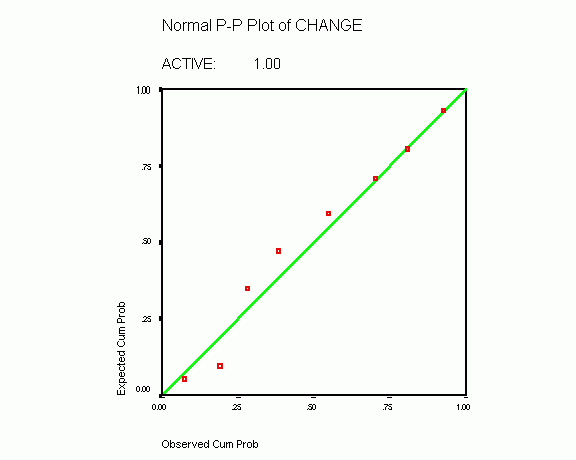
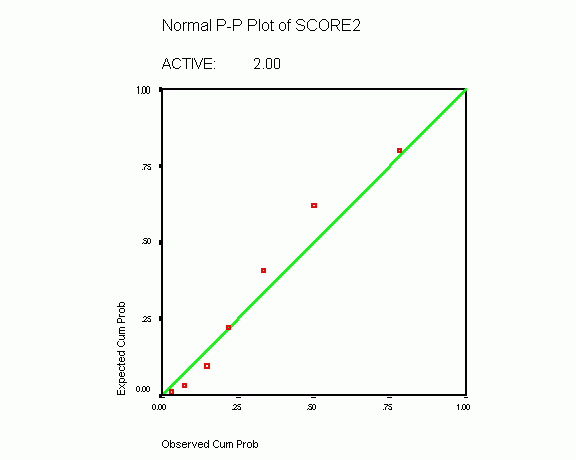
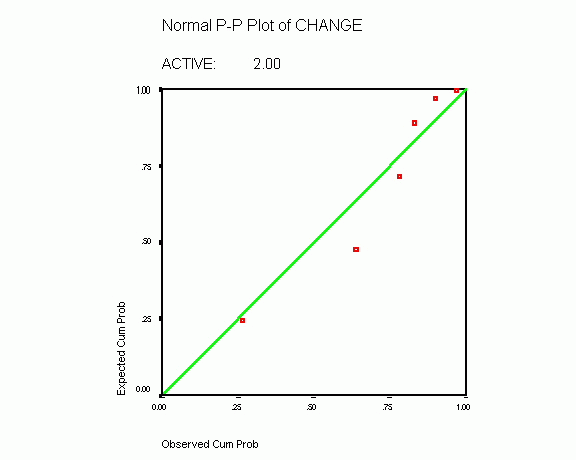
MODEL:  MOD_1.
 
Expected Normal quantiles calculated using Blom's proportional
estimation formula and assigning the mean to ties.

 
 
ACTIVE:         1.00
 
For variable SCORE2...
 
Normal distribution parameters estimated: location=4.3793103 scale=3.1443122
 
For variable CHANGE...
 
Normal distribution parameters estimated: location=5.2413793 scale=3.2365675

 
 
ACTIVE:         2.00
 
For variable SCORE2...
 
Normal distribution parameters estimated: location=8.4285714 scale=1.8593394
 
For variable CHANGE...
 
Normal distribution parameters estimated: location=1.0952381 scale=1.5781243
 

 

Normal p-p plot of score2 ; active= 1.00

Normal p-p plot of change ; active= 1.00

Normal p-p plot of score2 ; active= 2.00

Normal p-p plot of change ; active= 2.00

T-Test

How to do this:

 

ACTIVE

N

Mean

Std. Deviation

Std. Error Mean

SCORE1

1.00

29

9.6207

.7277

.1351

2.00

21

9.5238

.8729

.1905

SCORE2

1.00

29

4.3793

3.1443

.5839

2.00

21

8.4286

1.8593

.4057

CHANGE

1.00

29

5.2414

3.2366

.6010

2.00

21

1.0952

1.5781

.3444

SPSS automatically performs Levene's test for equality of variances. It also gives the results of two different T-tests, the standard t-test and the Welch t-test. The Welch t-test is simply a test that adjusts the degrees of freedom in a way that accounts for the inequality of the variances.


Levene's Test for Equality of Variances

t-test for Equality of Means

F

Sig.

t

df

Sig. (2-tailed)

Mean Difference

Std. Error Difference

95% Confidence Interval of the Mean

Lower

Upper

SCORE1

Equal variances assumed

.597

.443

.427

48

.671

9.688E-02

.2268

-.3591

.5528

Equal variances not assumed



.415

38.273

.681

9.688E-02

.2335

-.3758

.5695

SCORE2

Equal variances assumed

4.458

.040

-5.264

48

.000

-4.0493

.7693

-5.5960

-2.5026

Equal variances not assumed



-5.695

46.418

.000

-4.0493

.7110

-5.4801

-2.6184

CHANGE

Equal variances assumed

8.901

.004

5.412

48

.000

4.1461

.7661

2.6058

5.6865

Equal variances not assumed



5.986

42.926

.000

4.1461

.6927

2.7491

5.5431

General Linear Model (ANOVA)

How to do this:

 

APPLY

Dependent Variable

1

SCORE1

2

SCORE2


APPLY


Value Label

N

ACTIVE

1.00


29

2.00


21

Effect

Value

F

Hypothesis df

Error df

Sig.

Noncent. Parameter

Observed Power(a)

APPLY

Pillai's Trace

.588

68.416(b)

1.000

48.000

.000

68.416

1.000

Wilks' Lambda

.412

68.416(b)

1.000

48.000

.000

68.416

1.000

Hotelling's Trace

1.425

68.416(b)

1.000

48.000

.000

68.416

1.000

Roy's Largest Root

1.425

68.416(b)

1.000

48.000

.000

68.416

1.000

APPLY * ACTIVE

Pillai's Trace

.379

29.291(b)

1.000

48.000

.000

29.291

1.000

Wilks' Lambda

.621

29.291(b)

1.000

48.000

.000

29.291

1.000

Hotelling's Trace

.610

29.291(b)

1.000

48.000

.000

29.291

1.000

Roy's Largest Root

.610

29.291(b)

1.000

48.000

.000

29.291

1.000

a Computed using alpha = .05

b Exact statistic

c Design: Intercept+ACTIVE
Within Subjects Design: APPLY


Mauchly's W

Approx. Chi-Square

df

Sig.

Epsilon(a)

Within Subjects Effect



Greenhouse-Geisser

Huynh-Feldt

Lower-bound

APPLY

1.000

.000

0

.

1.000

1.000

1.000

Tests the null hypothesis that the error covariance matrix of the orthonormalized transformed dependent variables is proportional to an identity matrix.

a May be used to adjust the degrees of freedom for the averaged tests of significance. Corrected tests are displayed in the layers (by default) of the Tests of Within Subjects Effects table.

b Design: Intercept+ACTIVE
Within Subjects Design: APPLY

Source

Type III Sum of Squares

df

Mean Square

F

Sig.

Noncent. Parameter

Observed Power(a)

APPLY

244.530

1

244.530

68.416

.000

68.416

1.000

APPLY * ACTIVE

104.690

1

104.690

29.291

.000

29.291

1.000

Error(APPLY)

171.560

48

3.574





a Computed using alpha = .05



Source

Type III Sum of Squares

df

Mean Square

F

Sig.

Noncent. Parameter

Observed Power(a)

APPLY

244.530

1.000

244.530

68.416

.000

68.416

1.000

APPLY * ACTIVE

104.690

1.000

104.690

29.291

.000

29.291

1.000

Error(APPLY)

171.560

48.000

3.574





a Computed using alpha = .05



Source

Type III Sum of Squares

df

Mean Square

F

Sig.

Noncent. Parameter

Observed Power(a)

APPLY

244.530

1.000

244.530

68.416

.000

68.416

1.000

APPLY * ACTIVE

104.690

1.000

104.690

29.291

.000

29.291

1.000

Error(APPLY)

171.560

48.000

3.574





a Computed using alpha = .05



Source

Type III Sum of Squares

df

Mean Square

F

Sig.

Noncent. Parameter

Observed Power(a)

APPLY

244.530

1.000

244.530

68.416

.000

68.416

1.000

APPLY * ACTIVE

104.690

1.000

104.690

29.291

.000

29.291

1.000

Error(APPLY)

171.560

48.000

3.574





a Computed using alpha = .05

Source

Transformed Variable

Type III Sum of Squares

df

Mean Square

F

Sig.

Noncent. Parameter

Observed Power(a)

APPLY

APPLY_1

244.530

1

244.530

68.416

.000

68.416

1.000

APPLY * ACTIVE

APPLY_1

104.690

1

104.690

29.291

.000

29.291

1.000

Error(APPLY)

APPLY_1

171.560

48

3.574





a Computed using alpha = .05

Source

Type III Sum of Squares

df

Mean Square

F

Sig.

Noncent. Parameter

Observed Power(a)

Intercept

6217.614

1

6217.614

1459.561

.000

1459.561

1.000

ACTIVE

95.134

1

95.134

22.332

.000

22.332

.996

Error

204.476

48

4.260





a Computed using alpha = .05

Crosstabs

How to do this:

 

Cases

Valid

Missing

Total

N

Percent

N

Percent

N

Percent

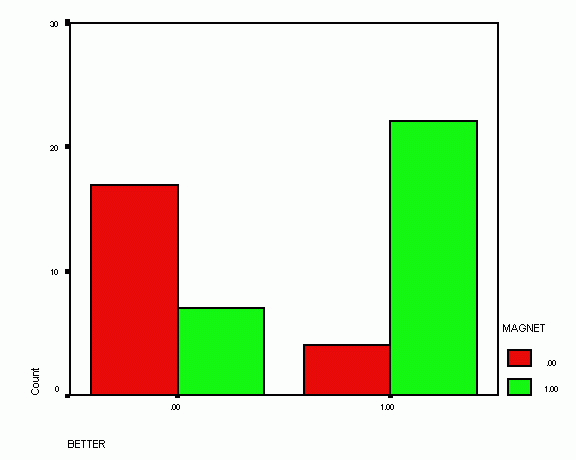
BETTER * MAGNET

50

100.0%

0

.0%

50

100.0%


MAGNET

Total

.00

1.00

BETTER

1.00

4

22

26

.00

17

7

24

Total

21

29

50


Value

df

Asymp. Sig. (2-sided)

Exact Sig. (2-sided)

Exact Sig. (1-sided)

Pearson Chi-Square

15.751(b)

1

.000



Continuity Correction(a)

13.557

1

.000



Likelihood Ratio

16.730

1

.000



Fisher's Exact Test




.000

.000

Linear-by-Linear Association

15.436

1

.000



N of Valid Cases

50





a Computed only for a 2x2 table

b 0 cells (.0%) have expected count less than 5. The minimum expected count is 10.08.

 

General Linear Model (ANCOVA)

ANCOVA to test the interaction of the covariate and factor.

How to do this

 

Value Label

N

ACTIVE

1.00


29

2.00


21

Source

Type III Sum of Squares

df

Mean Square

F

Sig.

Noncent. Parameter

Observed Power(a)

Corrected Model

219.364(b)

3

73.121

10.308

.000

30.923

.997

Intercept

.526

1

.526

.074

.787

.074

.058

ACTIVE

4.330

1

4.330

.610

.439

.610

.119

SCORE1

8.742

1

8.742

1.232

.273

1.232

.193

ACTIVE * SCORE1

10.645

1

10.645

1.501

.227

1.501

.224

Error

326.316

46

7.094





Total

2394.000

50






Corrected Total

545.680

49






a Computed using alpha = .05

b R Squared = .402 (Adjusted R Squared = .363)

General Linear Model (ANCOVA)

ANCOVA for main effects, no interaction.

How to do this

 


Value Label

N

ACTIVE

1.00


29

2.00


21

Source

Type III Sum of Squares

df

Mean Square

F

Sig.

Noncent. Parameter

Observed Power(a)

Corrected Model

208.719(b)

2

104.359

14.556

.000

29.113

.998

Intercept

.442

1

.442

.062

.805

.062

.057

ACTIVE

204.199

1

204.199

28.482

.000

28.482

.999

SCORE1

9.009

1

9.009

1.257

.268

1.257

.196

Error

336.961

47

7.169





Total

2394.000

50






Corrected Total

545.680

49






a Computed using alpha = .05

b R Squared = .382 (Adjusted R Squared = .356)