Chapter: Section: Home | Previous Section | Next Section VideoVariance Sum Law I
Author(s)
David M. Lane
Prerequisites
Variance
Learning Objectives
- Compute the variance of the sum of two uncorrelated variables
- Compute the variance of the difference between two uncorrelated
variables
As you will see in later sections, there are many
occasions in which it is important to know the variance of the
sum of two variables. Consider the following situation: (a) you
have two populations, (b) you sample one number from each population,
and (c) you add the two numbers together. The question is, "What
is the variance of this sum?" For example, suppose the two
populations are the populations of 8-year-old males and 8-year-old females in Houston, Texas, and that the variable of interest is
memory span. You repeat the following steps thousands of times:
(1) sample one male and one female, (2) measure the memory span
of each, and (3) sum the two memory spans. After you have done
this thousands of times, you compute the variance of the sum.
It turns out that the variance of this sum can be computed according
to the following formula:
where the first term is the variance of the sum,
the second term is the variance of the males and the third term
is the variance of the females. Therefore, if the variances on
the memory span test for the males and females were
0.9 and 0.8 respectively, then the variance of the sum would be 1.7.
The formula for the variance of the difference between
the two variables (memory span in this example) is shown below.
Notice that the expression for the difference is the same as the formula
for the sum.
More generally, the variance sum law can be written
as follows:
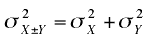
which is read: The variance of X plus or
minus Y is equal to the variance of X plus the variance of Y.
These formulas for the sum and
difference of variables given above only apply when the variables
are independent.
In this example, we have thousands of randomly-paired
scores. Since the scores are paired randomly, there is no relationship
between the memory span of one member of the pair and the memory span
of the other. Therefore the two scores are independent. Contrast
this situation with one in which thousands of people are sampled
and two measures (such as verbal and quantitative SAT) are taken
from each. In this case, there would be a relationship between
the two variables since higher scores on the verbal SAT are associated
with higher scores on the quantitative SAT (although there are
many examples of people who score high on one test and low on
the other). Thus the two variables are not independent and the
variance of the total SAT score would not be the sum of the variances
of the verbal SAT and the quantitative SAT. The general form of
the variance sum law is presented in a section
in the chapter on correlation.
Please answer the questions:
|